みなさんは、関数電卓を使ったことがありますか?

関数電卓は、簡単に言えば、単純な足し算・引き算・掛け算・割り算以外の計算ができる電卓です。分数、三角関数、角度、時間、複素数など、通常の電卓にはできない計算が、電卓と同じようにボタン入力だけで行えます。
多分「ある!」と答える人のほうが、少ないのではないでしょうか。そもそも関数電卓って何??という方もいるかもしれません。
電卓って日本の教育ではあまり重視されてない傾向
その原因には、学校の授業で、電卓が積極的に使われていないことが、ひとつあげられるでしょう。

私は日頃、研究論文を読むのが好きでいろいろ漁っているのですが……その中にあった清水克彦氏の『初等中等段階の算数・数学教育における電卓の活用の現状と課題』(コンピュータ&エデュケーション 13巻 2002 特集「計算機と数学教育」)によれば、日本は欧米と比べて、算数の授業で電卓があまり使われていません。
たしかに私も、学校の授業で電卓を使ったことはほとんどありませんでした。電卓が積極的に用いられていないのであれば、関数電卓になじみがないのも自然なことです。
カシオの関数電卓「fx-375ESA-N」を実際に触ってみた
……と語りましたが、かくいう私も一回も触ったことがありません。
文系の人間というのもあって、必要性を感じていなかったからです。
ただ今回、ちょっと触ってみたい気持ちが上回りまして……購入してみました。

機種は、Amazonでベストセラー一位を獲得しているカシオの関数電卓、fx-375ESA-Nです。ちなみに価格は、2020年11月現在、Amazonで約2,000円でした(案外安かったのも購入の決め手です)。
サイズは、少し大きめのスマホくらいですね。
こちらは、付属品のケースです。

このように本体を裏返しにはめることもでき、かばんに入れても誤作動しません。液晶画面が傷つかないのも嬉しい。
電源は、ソーラーとボタン電池のTWO WAY POWERです。電池寿命も3年とあるので、必要になったときに「付かない!」というのは、よほどのことがないかぎりないでしょう。
さて……

関数電卓を見たことがない人は驚くかもしれませんが、関数電卓には普通の電卓にはないボタンがたくさんあります。
左上にある「CALC」はカルク機能を使うためのボタンです。

カルク機能を使えば、変数を含む計算式(A=X2+2Y+5など)の答えを簡単に求めることができます。
右の真ん中あたりにある「sin」「cos」「tan」は、三角関数でおなじみの言葉ですね。サイン(正弦)、コサイン(余弦)、タンジェント(正接)のことです。

これらを用いれば、たとえば余弦定理(a2=b2+c2-2bc・cosA)の答えを、即座に求めることができます。
また、先程の関数電卓の写真を見てもらうとわかるように、ボタンの隙間にも、黄色や赤色でたくさんの文字が書かれています。
これもfx-375ESA-Nを使う上で、ポイントとなる機能で、簡単に言うと、各ボタンに搭載された裏機能です。

左上にある黄色で書かれた「SHIFT」ボタンを押せばボタン上の黄色で書かれた機能が、赤色の「ALPHA」ボタンを押せばボタン上の赤色で書かれた機能が使えます。
たとえば、「SHIFT」を一回押してから「sin」ボタンを押すと、「sin-1」を呼び出せます。「ALPHA」を一回押してから「 )」を押せば、変数を含む計算式などで用いる「X」を入力することができます。
fx-375ESA-Nは、こうした多数の機能をすぐに呼び出せるおかげで、さまざまな計算式を手早く作れます。
たとえば、A=X2+2Y+5という計算式があって、X=3、Y=2と決まっていたとしましょう。この場合、次のように入力すれば答えが出ます。
また、三角形ABCがあって、辺ABの長さが60センチ、辺BCの長さが100センチ、それら2辺の間に挟まれる角Bの角度が60度のとき、辺ACの長さは、次のように入力すると短時間で答えが求められます(「余弦定理」を使う)。
計算式:
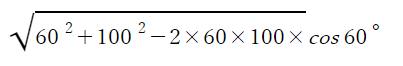
このように、関数電卓は直感的な操作で入力できるのが特徴です。
これ以外にも、fx-375ESA-Nには、前の計算式を呼び出す機能をはじめ、さまざまな機能があります。
関数電卓を触って気づいたこと
関数電卓を触っていると、彼の優秀さに驚かされます。
5/12+22/7のような、手計算だと面倒な計算の答えを、瞬時に出してくれるだけではありません。

関数電卓があれば、100m先の地点にボールを届かせたいと思ったときに、必要なボールの速さや必要な角度がわかります。ものさしでは絶対に測れない、遠く離れた星までの距離も瞬時に出せます。
私たちが、普段何気なく見過ごしている現象を、彼はささっと数字で示してくれるのです。
ただし、使いこなすためには、数学の知識が求められます。

逆数、乗数、平方根、三角関数、指数、対数、進数、複素数……などさまざまな概念の理解、かつそれらにまつわる公式の把握も必要です。なくても使えますが、それだと普通の電卓と変わりません。
『大学生・エンジニアのための関数電卓活用ガイド』(遠藤雅守著 森北出版 2018)という書籍を読んでも、具体的な関数電卓の使い方と同じくらい、概念や公式の説明が重点的に説明されています(この本で紹介しているカシオの機種は別のものですが、共通している部分は多く、入力の仕方も省略せずに書かれているのでおすすめです)。
また、“問題を読み直す力”も重要です。

そもそも、数学の知識以前に、この力がないと関数電卓のボタンをひとつも押せないからです。
ちょっと難しいですが、数学の問題2つを紹介
たとえば、先の書籍の中に、次のような問題があります。
| 銀行に毎年3.0%の複利で80万円を預けた。 これが100万円になるまでには何年待つ必要があるか。 『大学生・エンジニアのための関数電卓活用ガイド』p.76 例題5.12 |
これは、関数電卓を使えば、すぐに答えが出ます。
しかし重要なのは、関数電卓を持ち出すまでの過程です。
先に、解答から見てみましょう。
| 毎年3.0%の複利というのは、1年ごとにいまある預金が1.03倍になるということです。すなわち問題は、80×(1.03)x=100となるxを求めよ、と翻訳できます。 ここで両辺のlogをとれば、 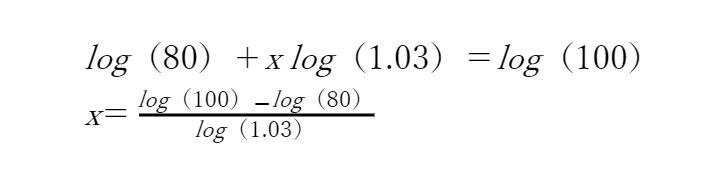 となり、あとは関数電卓で計算するだけです。 『大学生・エンジニアのための関数電卓活用ガイド』 p.76-77 |
注目すべきは最初の文章です。
関数電卓で答えを求めるために、『毎年3.0%の複利というのは、1年ごとにいまある預金が1.03倍になるということ』と読み直しています。
それによって「80×(1.03)x=100」という計算式を導き出し、答えを出しています。

もうひとつ問題を紹介しましょう。
水平の天井から、2本のひもで吊るされているライトを想像してください。天井に対するひもの角度をθとします。
| 天井から2本のひもで吊るされたライトがある。 ライトの質量をm=3.0kg、重力加速度の大きさをg=9.8m/s2、θ=30°として、2本のひもそれぞれに加わる張力Tを求めよ。 『大学生・エンジニアのための関数電卓活用ガイド』 p.43 例題4.3 一部省略) |
この問題に対する解答は、次のとおりです。
| ライトにはたらく力は、鉛直下向きの重力と2本のひもの張力です。物体が静止しているとき、物体にはたらく力は釣り合っています。 水平方向の力は対象で打ち消し合っているのは自明ですから、いまは鉛直方向の釣り合いだけを議論すれば十分です。 張力を鉛直方向と水平方向に分解して、鉛直方向の力の釣り合いの式を立てると、 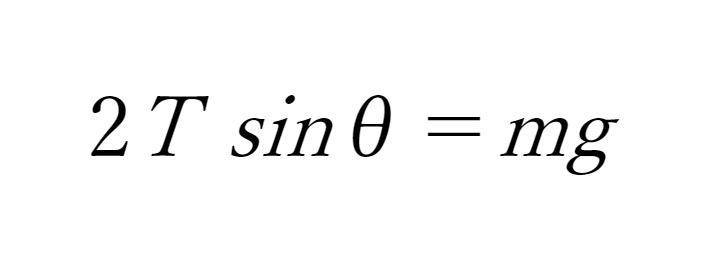 が得られ、これをTについて解けば、 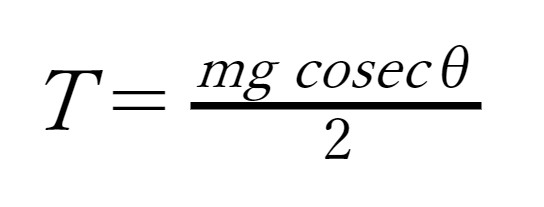 を得ます。 『大学生・エンジニアのための関数電卓活用ガイド』 p.43 ※ただし、cosecθの計算が直接できないため、実際はT=mg2sinθにする。 |
やや複雑ですが、これも先の問題と同じです。
問題文から『水平方向の力は対象で打ち消し合っているのは自明』であると判断し、「2本のひもそれぞれに加わる張力Tを求めよ」を「鉛直方向の力の釣り合いの式からTを求めよ」と読み直し、はじめて関数電卓を使っています。
つまり、いかに関数電卓という便利なツールがあったとしても、問題を読み直すことができなければ、そのツールを使うところに辿り着けないのです。
公式を丸暗記したところで、日常生活に応用できないのと同じでしょう。
“問題を読み直す力”は日常の困りごとを解決するときにも役立つ
世界的大ベストセラー『7つの習慣』の著者、スティーブン・R・コヴィーは、パラダイムシフトの重要性を説いています。

パラダイムとは、簡単に言えば、ものの見方です。
私たちは自分たちのこれまでの経験によって、自分でも気づかないほどに物事の見方が決定されています。
コヴィーは、問題を根本から解決したいのであれば、今持っているパラダイムが問題に対する見方そのものを歪めていないか確認し、それをシフト(読み直して変革していこう)、というわけです。
たとえば「アルバイトがすぐに辞めないようにするためには、どうしたらいいのか」は、「アルバイトが『来月も働こう』と思ってもらうには、どういう職場環境にすればいいのか」と読み直してみる。
こう考えると、アルバイト教育の方法だけでなく、アルバイト教育ができる環境の改善案もすぐさま思い浮かびます。

あるいは、「競合が強く、自社のサービスのアピールがうまくできていない。顧客を増やすためにはどうしたらいいのか」という問題があったとします。
これについて、「競合の手が届いていない市場に、自社も進出できていない。そのためには何をしたらいいのか」と読み直してみる。
そうすれば、市場の調査に向ける手立てが、解決策の候補に上がるでしょう。
このように、“問題を読み直す力”は、関数電卓に必要な力にとどまりません。
そしてちょっとだけ大げさに表現すると、関数電卓は、日常の困りごとを解決する力を磨くのに適したツール、とも言えるでしょう。使いこなそうとすればするほど、問題を読み直さなければいけないからです。

「一生縁がないと思っていた関数電卓が、日常の困りごとを解決するには“問題を読み直せばいい”と教えてくれた」
これが、関数電卓を触ったことで私が得られた知見です。
※こちらの記事の内容は原稿作成時のものです。
最新の情報と一部異なる場合がありますのでご了承ください。
この記事を書いたひと

フリーライター、元書店員。趣味は散歩やDIY。百均やホームセンターがテーマパーク並に面白いことに気づきました。【時間】についてひっそりと研究中です。 Twitterやっています。